(PR)
実質年率表記と元利均等払いの計算
クレジットカードの分割払いやリボルビング払いには、元金に金利が上乗せされます。
分割払いやリボ払いで適用される金利の表記には、実質年率が使用されています。カード会社から届いたサービス案内に分割払いやリボ払いの実質年率が記載されているはずです。
実質年率が「15.00%」と記載されていれば、1年間の利率は15%ということです。
元利均等払いの計算
例えば、クレジットカードで10万円の買い物をし5回払いにした場合、実質年率が15%だと1ヶ月当たりの利率は1.25%になります。
分割払いに元金と利率を合計した支払額が、毎回同額になる元利均等払いをあらかじめ指定していた場合には、月々の支払額と金利は以下のようになります。
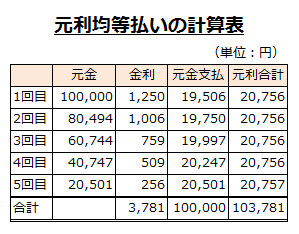
毎月の支払合計額は20,756円です。最終回だけ、端数の調整のため20,757円となっています。
1回目の支払額に含まれる金利は、100,000円に1.25%を乗じた1,250円です。そして、元利合計の支払額が20,756円なので、そこから金利1,250円を差し引いた19,506円が元金の減少額になります。
したがって、1回目の支払いを終えた後の元金の残高は80,494円です。
元利合計額の計算
毎月の元利合計額の計算は、まず「1」に金利0.0125を加えた1.0125を各支払回数だけ乗じていきます。
そして、5回分の計算結果を全て足すと、5.1907になります。
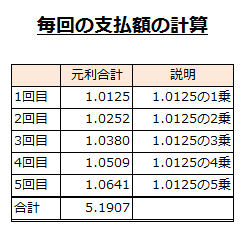
上の表を基に毎月の支払額を計算すると20,756円になります
- 毎月の支払額=(1回目金利+元金)/5.1907+1回目金利
上の計算式に具体的な数字を当てはめます。
- (1,250円+100,000円)/5.1907+1,250円=20,756円
あとは、毎月初の残高に利率1.25%を乗じた金利を20,756円から差し引いた金額分だけ毎月末の残高を減らしていきます。
アドオン表記
上記のような金利計算を毎回行っていたのでは、手間がかかりすぎます。そのため、実務では、分割払いの元利均等額の計算にアドオン表記を用いています。
アドオン表記は、実質年率ごとに分割払いの回数に応じた分割係数が記載されています。例えば、実質年率が15.00%で5回払いの場合、分割係数は3.78%です。
元金100,000円で実質年率15%、支払回数5回の場合、分割係数を利用すると、毎回の元利支払合計額は以下のようになります。
- (100,000円×1.0378)/5回=20,756円
上で表を作って計算した場合と、毎回の元利支払合計額が一致しています。
このようにアドオン表記は、電卓があれば簡単に計算できるので、店員が分割払いの相談を受けた時に素早く対応できます。
